Les trucs à savoir :
– Un graphique est un dessin en deux dimensions : sa largeur et sa hauteur.
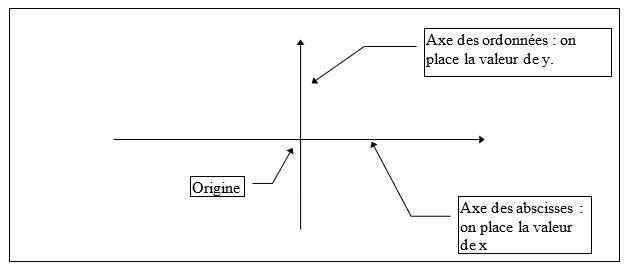
– Pour pouvoir placer un point sur un graphique, il faut connaître ses coordonnées.
Les coordonnées d’un point sont au nombre de deux (car il y a deux dimensions) :
La coordonnée horizontale que l’on appelle l’abscisse :
c’est la valeur de x (penser aussi à absciXe).
La coordonnée verticale que l’on appelle l’ordonnée :
c’est la valeur de y.
Une des difficultés est pour beaucoup de gens de se rappeler si les x c’est horizontal ou vertical (pareil pour y).
- Pour pouvoir placer un point sur un graphique, il faut se repérer dans le graphique, c’est pourquoi il faut tracer un repère (grâce à deux axes perpendiculaires), qui lui-même possède une origine, c’est la base du graphique.
A ce sujet les mathématiciens emploient des noms bizarres, style : repère « orthonormé », « orthonormal », « orthogonal ». N’ayez pas peur, le mot « ortho » signifie simplement que les 2 axes vont être à angle droit, c’est tout. C’est comme l’orthodentiste qui remet nos dents droites ou l’orthopédiste, qui nous apprend à marcher droit… facile non ?
- En résumé :
Comment réaliser un graphique soigné ?
1) Il me faut du papier millimétré.
2) Il me faut un crayon gris bien taillé.
La preuve :

3) Je dois savoir quelles sont les limites de mon graphique :
- Quelle est la plus petite valeur que prendra x ?
- Quelle est la plus grande valeur que prendra x ?
- Quelle est la plus petite valeur que prendra y ?
- Quelle est la plus grande valeur que prendra y ?
En effet, il ne sert à rien de faire aller l’axe des x jusque 50, si sa plus grande valeur est 20.
4) Je dois occuper le plus grand espace possible sur ma feuille de papier millimétré : mon graphique sera alors encore plus précis.
5) Si mon graphique a été fait à partir d’un problème, je ne dois pas oublier d’inscrire la légende :
Que représente l’axe des x ?
Une somme en euros ? Des kilomètres parcourus ? …
Que représente l’axe des y ?
Une somme en euros ? Un prix de revient ? Un bénéfice ? …
6) Lorsque je place des points sur mon graphique, je les représente par un +, à la rigueur par une croix et surtout pas par . ou * :

Prenons deux exemples, pour nous entraîner :
Exemple 1 :
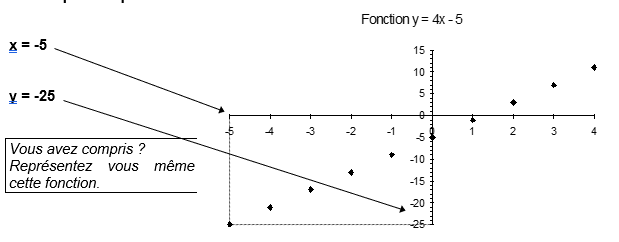
Nous allons tracer le graphique de la fonction y = 4 x – 5 (voir plus loin ce qu’est une fonction)
Le tableau est :
x | – 5 | – 4 | -3 | – 2 | – 1 | 0 | 1 | 2 | 3 | 4 |
y | – 25 | – 21 | – 17 | – 13 | – 9 | – 5 | – 1 | 4 | 7 | 11 |
(voir au besoin fiche outil – comment calculer certaines valeurs d’une expression algébrique)
Le graphique sera :
Exemple 2 :
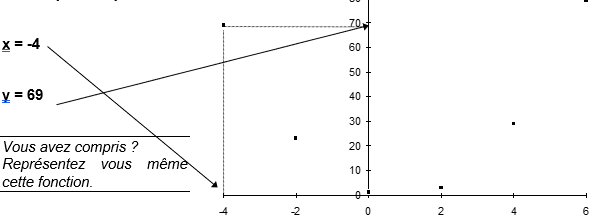
Nous allons tracer le graphique de la fonction y = 3x2 -5x + 1.
(voir au besoin fiche outil – comment calculer certaines valeurs d’une expression algébrique)
x | – 4 | – 2 | 0 | 2 | 4 | 6 |
y | 69 | 23 | 1 | 3 | 29 | 79 |
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
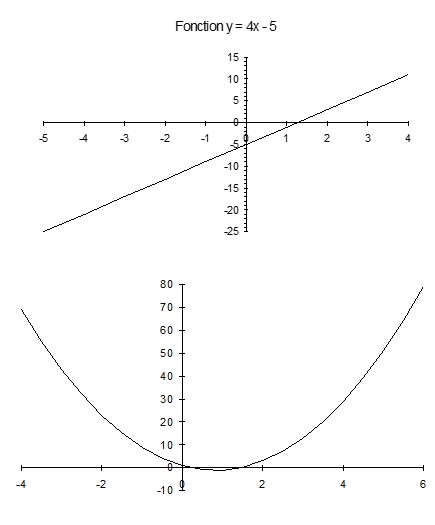
Relier les points d’un graphique : Exemples
Lorsque l’on a placé les points, très souvent il faut les relier.
Comment ?
- Si le graphique a l’apparence d’une droite, on relie les points à la règle et surtout pas à main levée, c’est à dire sans règle.
- Si le graphique n’a pas l’apparence d’une droite, on relie les points à main levée et surtout pas avec une règle.
Reprenons les deux graphiques précédents :
Fondateur de différents sites dont tableaunumerique.net, concours-atsem.fr, trouvix.fr ou encore laboiteaconcours.com Frédéric fait partie du collectif Profbook.fr.
Besoin de cours particuliers ou d’une remise à niveau en maths ? C’est ici ! Cours particuliers de Mathématiques à distance et en présentiel niveau primaire, collège et Prépa Concours








