20 avril 2022, 17h14, vous venez de prendre votre goûter : 1 croissant acheté 2€50 chez votre boulanger. Vous décidez de passer une fin de journée détente dans votre canapé, devant le 13ème épisode de la 2ème saison de votre série du moment. Avant que le générique ne se lance, vous avez déjà les genoux réquisitionnés par vos 2 chats entrelacés l’un sur l’autre.
Vous ne remarquez rien de particulier, dans cette journée ordinaire pour beaucoup ? C’est normal, nous y sommes tellement confrontés que nous n’y faisons plus forcément attention au quotidien. Et pourtant, c’est une des capacités essentielles de l’humanité : la faculté de compter, de manipuler les nombres. Mais comment en sommes-nous arrivés là ?
Annie propose des accompagnements en maths pour les lycéens (https://mathswinners.fr/) depuis plus de 20 ans. Elle a bien voulu partager avec nous l’histoire des nombres et de leur utilisation.
-Bonjour Annie. On entend souvent dire que « les maths ça ne sert à rien », qu’en pensez-vous ?
-Les nombres, et les maths en général, sont présents partout autour de nous. L’heure, la date ou les prix en sont des exemples simples du quotidien. En fait, on les trouve même dans la nature elle-même. Les coquilles d’escargots ou les fleurs de tournesol par exemple semblent coller à la spirale de Fibonacci.
-Qu’est-ce que c’est que cette spirale de Fibonacci ?
-C’est une spirale formée grâce à la suite de Fibonacci : une suite de nombres dans laquelle chaque nombre se calcule en faisant la somme des deux précédents. On part de 0 et 1, puis 0+1 qui font 1, 1+1 = 2, 1+2 = 3, 2+3=5, etc… Soit 0 1 1 2 3 5… Pour tracer la spirale, on utilise des carrés avec des côtés qui prennent successivement la taille de chaque nombre de cette suite, comme ceci :
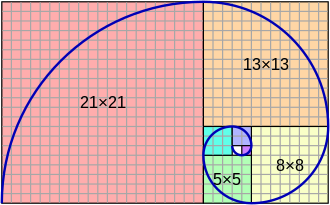
-La nature colle donc aux maths ?
-Ce sont plutôt les maths qui collent à la nature. Prenez notre façon de compter. On compte par « paquets » de 10 : les chiffres de 0 à 9, les dizaines sont des groupes de 10, les centaines, des groupes de 100, c’est-à-dire 10 groupes de 10… Ce n’est pas un hasard. Nous avons 10 doigts, c’est sans doute ce qui a poussé nos ancêtres à compter de la sorte. D’ailleurs, vous savez sans doute compter sur vos doigts, mais saviez vous que vous pouviez compter jusqu’à 156 avec vos mains ? (https://mathswinners.fr/utiliser-son-corps-pour-compter/) Et même faire des multiplications ?
-Jusqu’à 156 ? J’en déduis qu’il y a d’autres façons de compter que de 10 en 10 ?
-Oui ! Certains peuples, comme les Maya, utilisaient aussi leurs doigts de pieds pour compter, et faisaient donc des « paquets » de 20. On dit qu’ils comptent en base 20. Nous comptons en base 10, donc avec des paquets de 10, tout comme le faisaient les Égyptiens de l’antiquité. Les sumériens et mésopotamiens, qui vivaient à la même époque que les Égyptiens, comptaient eux en base 60. D’ailleurs, il nous arrive aussi de compter en base 60 : lorsqu’il s’agit de l’heure. Il y a 60 secondes dans 1 minute, et 60 minutes dans 1 heure.
-D’autres animaux ont également des « doigts », est-ce qu’ils comptent, eux aussi ? Et ceux qui n’ont pas de doigts ?
-Les animaux auraient des notions de nombre, en effet, notamment 1, 2 et « plusieurs ». Comme nos ancêtres. Avant de maîtriser le calcul, ils avaient vraisemblablement cette notion du solitaire, du couple et du groupe, sans forcément aller dans le détail. En fait, si on y réfléchit un peu, les chiffres sont quelque chose de très abstrait, c’est un concept. Vous n’avez jamais vu « trois ». Ce que vous voyez, c’est la représentation du chiffre tel qu’on l’écrit (et là, un romain, par exemple, ne verrait donc pas la même chose : quand vous voyez « 3 », lui verrait « III »). Vous pouvez aussi vous représenter trois chats. Mais la notion de « trois » en elle-même ne représente rien concrètement.

-Comment avons-nous commencé à utiliser ces notions, dans ce cas ?
-L’humanité a commencé à compter en utilisant des objets : ses doigts, des cailloux ou encore en gravant des traits. C’est quelque chose qui ne nécessite pas de savoir réellement compter. Il suffit d’associer un caillou ou un trait à un élément que vous voulez compter. Par exemple, vous voulez vous assurer que tous vos moutons sont bien rentrés le soir. Vous pouvez savoir combien vous en avez et les compter un par un, mais vous pouvez également utiliser des cailloux. Le matin, lorsqu’ils sortent, vous ajoutez un caillou dans une pile pour chaque, et quand ils rentrent le soir vous en retirez un pour chacun. S’il vous reste des cailloux dans votre pile, c’est que visiblement vous avez un problème !
-Si cette méthode marchait bien, qu’est-ce qui a poussé les Hommes à changer de technique ?
-Les cailloux marchent bien pour de petites quantités. Quand on commence à devoir manipuler de plus grands nombres, cela devient tout de suite beaucoup compliqué.
-C’est là qu’ils ont inventé les nombres ?
-Il est plus probable en fait qu’ils aient commencé à faire des paquets. Disons que 10 petits cailloux fassent un moyen caillou, et 10 moyens un gros. De ces objets physiques ont découlé des représentations gravées de ces objets, puis enfin des symboles détachés de toute représentation physique.
-Mais avec ces représentations anciennes, ils ne pouvaient faire que des additions ou des soustractions, non ?
-C’est une idée reçue ! En vérité, les peuples de l’antiquité avaient déjà une très bonne connaissance des mathématiques. Ils savaient faire des additions et soustractions, oui, mais également des multiplications et des divisions. Ils connaissaient les fractions, et savaient même résoudre des équations à plusieurs inconnues. En fait, ils avaient besoin des maths, pour l’agriculture, déjà, où ils devaient calculer et départager les surfaces, suivre l’évolution des productions, mais également pour l’architecture, avec des bâtiments de plus en plus complexes, l’astronomie ou encore les calendriers.
-C’est donc la « vraie vie » qui a complexifié les maths ?
-Elle n’a pas vraiment « complexifié » les maths, non. Mais c’est elle qui a poussé les savants à chercher de nouveaux outils pour résoudre les problèmes qu’ils avaient devant eux. Prenez le grec Thalès, par exemple. Vous le connaissez sans doute, c’est son théorème qui permet de calculer la taille d’un côté d’un triangle manquant à l’aide d’un autre triangle. En fait, selon une légende, il aurait développé son théorème pour répondre au défi du Pharaon d’Egypte. Ce dernier lui aurait demandé de calculer la hauteur de la pyramide de Khéops. Une inconnue : la hauteur de la pyramide. 3 distances connues : la taille du savant et celles de leurs ombres respectives.
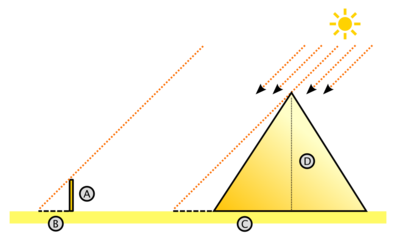
-Et c’est comme ça qu’il a gagné le défi ?
-Cette histoire n’est sans doute qu’une légende, mais il est facile ainsi de calculer la hauteur de différents monuments. Vous connaissez sûrement d’autres noms de savants, antiques ou non, qui ont marqué les maths : Pythagore, Fibonacci dont j’ai parlé tout à l’heure ou encore Euclide, et sa division euclidienne.
-On parle parfois de « chiffres arabes » quand on évoque nos nombres, ils ont donc été « importés » en Europe, c’est ça ?
-C’est exact. Ils seraient inspirés d’une numération indienne datant du IIIe siècle avant notre ère. Ils sont ensuite repris par un mathématicien arabe, aux environs du IXe siècle. Pendant ce temps, en Europe, nous en étions encore à utiliser les chiffres romains. Ce n’est qu’au Xe siècle qu’ils ont atteint l’occident, mais ils sont d’abord interdits pour les documents officiels. Ils ne remplaceront les chiffres romains qu’à la Renaissance, à partir du XVe siècle.
-Et ils n’ont plus changé depuis ?
-Non, nous les utilisons encore de nos jours. Mais l’écriture romaine n’a pas non plus disparu, puisqu’on l’utilise encore aujourd’hui notamment pour écrire les siècles.
-Hé bien, merci pour ce rapide voyage à travers le temps.
Professeur particulier en Maths et formatrice depuis plus de 30 ans, Annie a accompagné plus d’un millier d’apprenants de 5 à 78 ans, sous différentes formes (cours particulier, cours magistral, animation de groupe hétérogène), dans différentes disciplines (mathématiques, français, bureautique, comptabilité, gestion de chantier, électricité, badminton) et pour différents niveaux (initiation, remise à niveau, perfectionnement).
Ces différentes expériences lui ont appris à définir les besoins de ses élèves, à créer des parcours spécifiques et à pratiquer une formation individualisée, adaptée aux difficultés de chacun.
En 2021 elle a créé un programme d’accompagnement destiné aux lycéens, plus efficace que les classiques cours de soutien scolaire et qui tient compte de la façon dont notre cerveau apprend : Maths Winners.(lien : https://mathswinners.fr)
Annie fait partie du collectif Profbook.fr. Si vous avez besoin d’aide en Maths, vous trouverez sa fiche ici : https://profbook.fr/listing/cours-de-maths-avec-annie/








