Les maths en prépa « non-scientifique »
Si vous êtes en prépa économique et commerciale (ECG) voire littéraire (BL), ou que vous l’envisagez, a priori ce n’est pas pour faire des maths votre carrière ni vos études à moyen terme. Beaucoup d’élèves dans ces filières souhaitent même carrément arrêter les maths ou faire en sorte de s’en servir le moins possible.
Et pourtant c’est bien cette matière qui peut faire toute la différence, pendant l’année (pour votre dossier) et jusqu’aux concours (et soyons réalistes, vous aurez besoin des maths ou des statistiques à moyen ou long terme, dans vos études ou votre travail). D’abord parce que nombre de vos camarades choisiront de ne pas y investir beaucoup de temps (dans la perspective des concours vous serez donc meilleur·e qu’elles et eux), ensuite parce qu’un peu de pratique et de méthodologie permettent de faire des progrès importants et surtout, rapides.
Ce que mon expérience de l’enseignement m’a montré par dessus tout, c’est qu’énormément d’étudiant·es de prépa ont très peu confiance en leurs capacités à faire des maths. Cet article présente quelques points de méthodologie et astuces qu’on n’apprend pas en classe et qui vous permettront de (re)trouver confiance en vous quand vous faites des maths.
1. Étudier (attentivement) l’énoncé
Ici, c’est l’expérience qui parle : la majorité des élèves (lycée, prépa et université confondus) lisent mal les énoncés. Résultats : ils et elles passent à côté d’indices essentiels à la résolution du problème. Un exemple :


Concentrez vous aussi sur le but recherché : il n’est pas demandé de trouver la solution de l’équation, seulement de montrer qu’elle existe. Économisez votre énergie et ne cherchez pas à la calculer (si on en a besoin plus tard dans l’exercice, on y reviendra à ce moment là).
N’hésitez pas à annoter l’énoncé pour garder en tête les éléments importants !

2. « Enchaîner » les questions en DS
Qu’on se le dise une bonne fois pour toute : vous n’arriverez JAMAIS à faire un DS de prépa (ni votre concours) en entier dans le temps imparti (sauf peut-être les premiers DS de première année). Moi non plus, le jury non plus (en tout cas pas en rédigeant tout comme il faut et avec le facteur stress).
Ce n’est pas le but. Le but (côté jury), c’est de distinguer les élèves selon la quantité de questions répondues. Donc votre but à vous, c’est de répondre à un maximum de questions. Dans l’ordre, dans le désordre, peu importe.
D’où ce second conseil : ne perdez pas votre temps quand vous bloquez sur une question, passez à la suite. Dans l’idéal, essayez de ne pas rester plus de 5 minutes (grand max) sans écrire. L’avantage des devoirs en prépa, c’est que même si on bloque à la première question on peut, dans de nombreux cas, répondre aux suivantes. Prenons cet exemple d’étude de fonction définie par une intégrale :
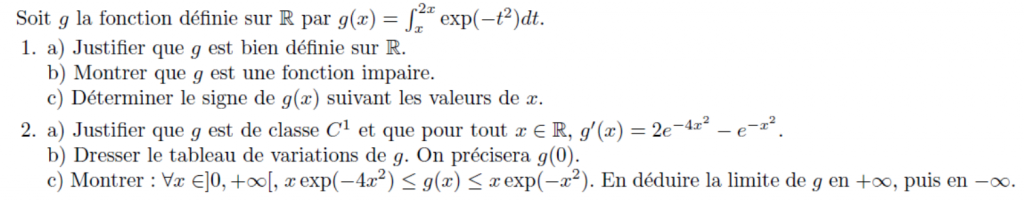
Imaginons que je bloque sur la question 1. L’énoncé me donne quand même pas mal d’informations sur : je connais son ensemble de définition (R) et je sais qu’elle est impaire, donc que sa courbe représentative est symétrique par rapport à l’origine du repère. On me donne même l’expression de sa dérivée : il ne reste plus qu’à étudier son signe pour répondre à la question 2(b) :
Notez que le tableau de variations est cohérent avec le fait que est impaire. De même, si je ne sais pas comment montrer l’inégalité donnée à la question 2(c), je peux quand même utiliser ce résultat pour trouver les limites de aux bornes de son ensemble de définition :


Ainsi, malgré mes blocages, j’ai tout de même répondu à quelques éléments de l’exercice ; je passe au suivant et je reviendrai sur les questions qui m’ont bloqué(e) s’il me reste du temps à la fin.
L’avantage d’« enchaîner » ainsi en DS, c’est que vous allez réaliser qu’il y a plein de questions auxquelles vous savez répondre. Elles vous assureront quelques points, et vous pourrez réfléchir au reste avec l’esprit plus tranquille (et plus de tranquillité = meilleures performances).
3. (Bien) travailler les corrections
Beaucoup de plateformes de cours particuliers et de profs proposent des ressources et exercices corrigés pour s’entraîner (par exemple ici ou ici). Il ne faut pas hésiter à les utiliser : faire des exercices avec la correction permet non seulement de vérifier ses résultats à la fin mais aussi (et surtout) de faire le plein d’idées pour avancer en cas de blocage. On peut même progresser en lisant des corrections d’exercices.
Mais pour que ce travail soit bénéfique à moyen terme (pour votre prochain DS), encore faut-il prendre le temps de bien les lire, et par là je veux dire les lire « activement » : en analysant les étapes, en prenant le temps de détailler les calculs, de déterminer les théorèmes et méthodes utilisés… Prenons l’exemple d’un calcul de somme :
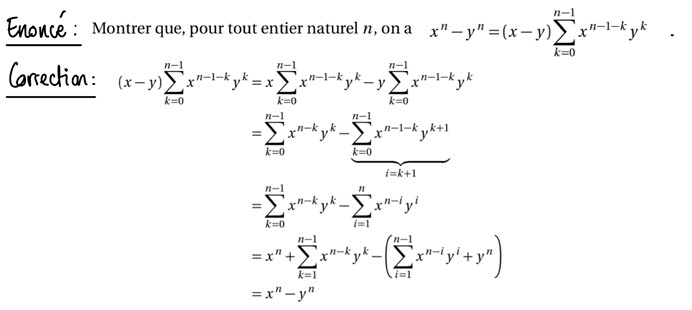
La correction est relativement détaillée, on voit qu’on part du terme de droite de l’égalité, qu’on fait un changement d’indice… En y passant quelques minutes, vous allez comprendre les calculs, mais serez-vous capable de les reproduire ? Avez-vous compris pourquoi il est préférable de démarrer par le terme de droite ? Quelle propriété utilise-t-on pour passer de la ligne 1 à la ligne 2 ? Une correction « travaillée » et annotée ressemblerait à ça :
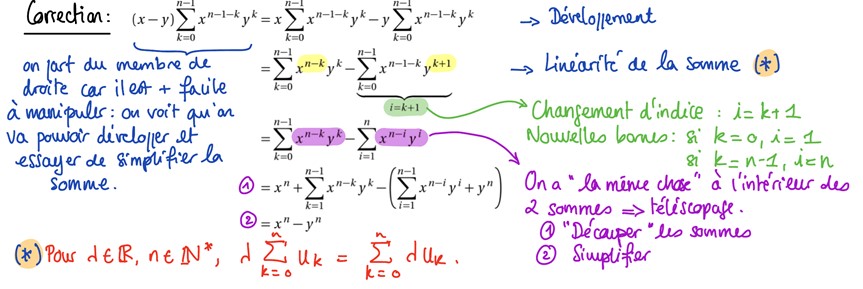
Détailler le pourquoi et le comment de chaque étape permet d’abord de les clarifier, ensuite de mémoriser les méthodes et les propriétés : vous serez maintenant capable de repérer d’un coup d’œil les sommes téléscopiques, vous vous tromperez moins dans les changements d’indice, vous penserez à utiliser la propriété de linéarité. Écrire le détail des corrections permet aussi d’y revenir plus tard facilement.
Remarque : Travailler des corrections, c’est très utile mais ça ne suffit pas : (re)faire des exercices sans correction reste une partie essentielle du travail en maths quelque soit le niveau.
4. Poser ses questions
Là, vous vous dites sûrement, « Merci du conseil Marie, on l’a déjà entendu 50 fois depuis le collège ». C’est vrai. Sauf que je suis toujours surprise de voir à quel point les étudiant·es ne posent JAMAIS (ou presque jamais) de questions en cours.
Pour faire court : posez vos questions. En classe, à la fin des cours, en colle, et en cours particuliers (si vous en prenez). Ne pas poser votre question (parce qu’elle vous semble « bête », que vous avez peur de déranger…) aura pour seul effet de vous bloquer et de diminuer votre confiance en vous.
Des moments privilégiés pour les poser sont les colles de maths : vous êtes en petit groupe avec un colleur (votre prof ou quelqu’un·e d’autre), vous avez le temps, ce n’est pas un DS donc il n’y a pas de gros enjeu si vous ne faites pas beaucoup d’exercices. Pour « rentabiliser » votre colle :
- Préparez-la (si possible) : la plupart des profs donnent le programme des colles en avance, voire des exercices qui y seront proposés. Si vous les faites en amont, vous avancerez plus vite le jour J sur les parties « faciles » et pourrez passer du temps et poser vos questions sur les points plus complexes.
- Faites des essais: même si vous ne savez pas trop comment aborder une questions, tentez un truc (un calcul, une propriété…). Les colles sont une excellente occasion de « pratiquer » les maths et votre colleur est là pour vous aiguiller en cas d’erreur.
Si vous appliquez les conseils de cet article, vous allez assez vite voir sur quel type de problème, sur quel chapitre vous avez le plus de difficulté. Vous pourrez ainsi mieux cibler vos questions, votre interlocuteur vous répondra de manière plus adaptée à votre profil, et vous apprendrez d’autant mieux.
5. S’exercer, s’exercer, s’exercer
Bon. J’ai menti.
Pour progresser en maths, il ne suffit pas d’« un peu » de pratique. Il en faut même beaucoup, et si vous ne deviez retenir qu’une seule chose de cet article ce serait : la clé, c’est la pratique.
Cependant, si vous appliquez à votre pratique régulière des maths les conseils ci-dessus, je vous promet que vous allez voir des résultats rapides. J’ai pu le voir avec mes élèves en cours particuliers : ces conseils font partie de ceux qui les ont les plus aidé·es.
Et si vous avez du mal à les appliquer, revenez au n°4 : posez vos questions, écrivez-moi.







