La soustraction est une opération qui permet de calculer une différence.
On utilise la soustraction pour calculer :
- Un reste
C’est le sens « enlever », celui qui est le plus facilement compris parce qu’intuitif.
- Il y a 12 oiseaux dans un arbre. 5 oiseaux s’envolent. Combien reste-t-il d’oiseaux dans l’arbre ?
- Un complément
C’est le sens « pour aller à ». Il correspond aux problèmes dans lesquels on cherche une partie quand on connait le tout et l’autre partie.
- J’ai 32 € dans mon porte-monnaie. Je veux acheter un jouet qui coûte 45 €. Combien me manque-t-il pour pouvoir acheter ce jouet ?
- Un écart ou une différence
C’est le sens qui concerne les problèmes de comparaison. Il est généralement plus difficile à appréhender parce que rien dans l’énoncé n’invite à utiliser une soustraction.
- Un train bleu a 15 wagons. Un train rouge a 11 wagons. Quel train a le plus de wagons et combien en a-t-il de plus ?
Pour trouver le résultat d’une soustraction, on ne recule pas systématiquement sur une file numérique. Si cette méthode peut fonctionner lorsqu’on retire un petit nombre (104 – 6) elle n’est plus du tout pertinente ni utilisable pour retirer un grand nombre (104 – 75).
Ainsi :
- Pour calculer mentalement 104 – 6 on effectue des retraits successifs : 104 – 4 – 2 = 100 – 2 = 98
- Pour calculer mentalement 104 – 75 on cherche les compléments successifs : de 75 à 100 (+25) puis de 100 à 4 (+4) soit 25 + 4 = 29 et donc 104 -75 = 29
Lorsque la soustraction est compliquée à calculer, on apprend à la poser. Mais il faut bien comprendre également que savoir poser une soustraction ne remplace pas le calcul mental qui est parfois plus efficace, plus rapide. Ainsi, poser 180 – 10 ne présente pas d’intérêt.
Afin que les élèves n’associent pas systématiquement la soustraction à une perte, il est important de présenter très tôt aux élèves :
- Des problèmes que l’on ne résoudra pas en faisant une soustraction alors qu’il y a dans l’énoncé l’expression de la perte.
Exemple : Pendant la récréation, Léo a perdu 8 billes. A la fin de la récréation il lui reste 13 billes. Combien Léo avait-il de billes avant la récréation ?
- Des problèmes que l’on résoudra en faisant une soustraction alors qu’il y a dans l’énoncé l’expression du gain.
Exemple : Pendant la récréation, Léa a gagné 7 billes. A la fin de la récréation, elle a 16 billes. Combien Léa avait-elle de billes avant la récréation ?
LES DIFFERENTES METHODES DE SOUSTRACTION
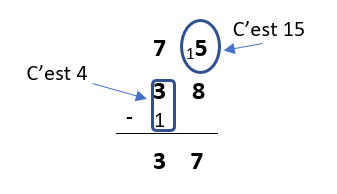
La méthode française « traditionnelle », par compensation :
Elle est basée sur la propriété mathématique de l’invariance d’une différence lorsqu’on ajoute simultanément le même nombre aux deux termes d’une soustraction.
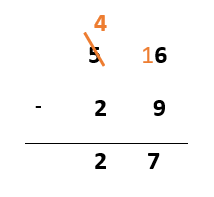
La méthode anglo-saxonne par emprunt ou « cassage » :
On casse une dizaine pour l’échanger contre 10 unités à la place (ou on casse une centaine pour l’échanger contre 10 dizaines)
AVANTAGES ET INCONVENIENTS DES METHODES DE SOUSTRACTION
| Technique traditionnelle | Technique par cassage |
Avantages | · Elle ne pose pas de problème aux parents d’élèves car en général c’est cette technique qu’ils ont apprise. · Elle est efficace quand il y a plusieurs retenues.
| · C’est la plus proche du système de numération. · Elle est facile à expliquer avec du matériel de numération. |
Inconvénients | · Elle manque de sens pour beaucoup d’élèves car il faut avoir compris la notion de conservation des écarts et les retenues ont un double sens. · Elle est complexe en termes d’écriture (place des retenues). | · Elle pose un problème de présentation (chiffres barrés -> le travail peut manquer de soin). · Elle est difficile à gérer quand il y a plusieurs retenues (notamment quand il y a un ou des zéros en haut). · Elle n’est généralement pas connue des parents d’élèves. |
Rédigé par Florence Conrozier, professeur de cours particuliers en ligne et en présentiel pour l’élémentaire et le collège.
https://www.linkedin.com/in/florence-conrozier-97444423b/
Retrouvez sa fiche Profbook pour ses cours particuliers ici : https://profbook.fr/listing/soutien-scolaire-et-approfondissement-de-lelementaire-au-college-avec-florence/














