Equation du 1er degré à une inconnue : définition
Une équation du premier degré à une inconnue est de la forme :
ax + b = 0
x est l’inconnue (il n’y a qu’une inconnue, même si on la rencontre plusieurs fois. Cette inconnue est au degré 1, voir cours « Monômes et polynômes »).
a et b des nombres donnés.
Résoudre l’équation ax+b=0, c’est déterminer l’ensemble S des nombres x qui vérifient cette équation.
Que signifie le mot "équation" ?
Prenez le temps de lire ce paragraphe, ça devrait vous débloquer pas mal de choses
(peut-être même que vous allez finir par aimer les maths).
La racine du mot « Equation », c’est « Egalité » mais aussi « Equilibre ». C’est justement ce mot qui va nous servir maintenant. Imaginez la vieille balance de nos grand-mères (ou plus), c’est-à-dire celle avec des plateaux (2 plateaux).
Si votre balance est en équilibre, c’est une équation.
Si elle penche d’un côté, c’est une inéquation.
Vous avez le droit de faire ce que vous voulez avec votre balance, je dis bien ce que vous voulez, je persiste et je signe d’ailleurs.
Il n’y a qu’une et une seule règle à respecter : votre balance doit toujours être en équilibre, sinon c’est perdu.
Comme vous avez l’air très sympathique, je vais vous donner un exemple :
C’est là que la balance prend toute son importance :
Admettons que l’on me dise : « la balance ci-contre est équilibrée. Un objet rouge pèse 5g. Combien pèse un objet bleu ? ».
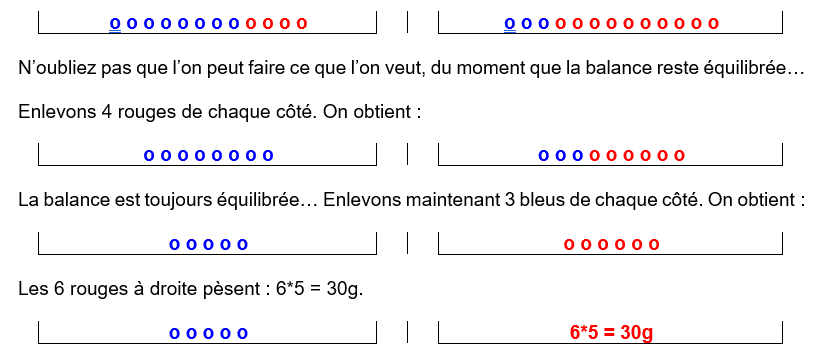
Donc les 5 bleus à gauche pèsent eux aussi 30g.
Donc 1 bleu pèse 30/5 = 6g.
Comment aurait-on traduit tout ceci mathématiquement ?
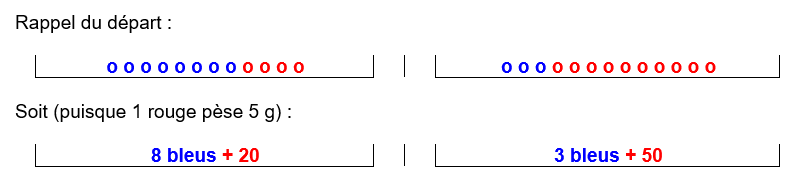
L’équation aurait donc été :
8 b + 20 = 3 b + 50
On enlève 20 de chaque côté :
8b + 20 – 20 = 3b + 50 – 20
Reste :
8b = 3b + 30
On enlève 3b de chaque côté :
8b – 3b = 3b + 30 – 3b
Reste :
5b = 30
On divise par 5 (des 2 côtés !!!!!!!!) :
5b/5 = 30/5
1b = 6
Ou encore : b = 6
Et voilà, c’est ça une équation. Ah oui ! Quand vous résolvez, forcez-vous à aligner verticalement le signe « = » : c’est l’aiguille de votre balance…
Exemple d’équation résolue :
6(x-2)+4 = 2(5-x)
6x-12+4 =10-2x
6x+2x-8 =10
8x -8 +8 = 10+8
8x =10+8
8x = 18
8x/8 = 18/8
x = 18/8
x = 9/4
S={9/4} ou S={2,25}
Cas particulier 1 : Equation-Produit
(2x-1) (x+7) = 0
A retenir : Un produit de facteurs (A*B=0) est nul si l’un au moins des facteurs est nul : A=0 ou B=0
2x-1 = 0 ou x+7= 0
2x = 1 x = -7
x = 1/2
S={-7;1/2}
Cas particulier 2 : Equation avec fractions
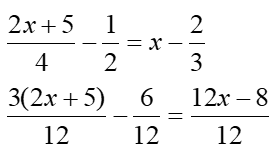
TOUTES les fractions doivent être au MEME dénominateur (le dénominateur que vous choisissez n’a pas d’importance, l’important étant d’avoir le même ABSOLUMENT PARTOUT) !!!
Ensuite, on enlève les fractions (n’oubliez pas qu’on fait ce que l’on veut, tant que la balance reste équilibrée)
3(2x+5) – 6 = 12x – 8
6x+15-6 = 12x-8
6x + 9 = 12x – 8
6x-12x+9-9 = 12x -8 -12x – 9
-6x = -8-9
-6x = -17
-6x / -6 = – 17/-6
x = -17/-6 = 17/6
S={17/6} ou S={2,83}
Cas particulier 3 : Equation-Quotient
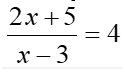
Remarque : comme on ne peut pas diviser un nombre par 0, pour que cette équation existe le dénominateur doit être différent de zéro : x-3<>0 soit x<>3. Cela signifie que si on trouve 3 comme solution, il faudra la déclarer IMPOSSIBLE.
Pour pouvoir la résoudre, il faut avoir un dénominateur identique partout.
On prend donc (x-3) comme dénominateur commun. Le membre de droite devient donc 4(x-3)/(x-3). Ensuite on enlève les dénominateurs. Il reste :
2x+5 = 4(x-3)
2x+5 = 4x-12
2x-4x+5-5 = 4x-12-5-4x
-2x = -17
x = -17/-2=17/2
S={17/2} ou S={8,5}
Fondateur de différents sites dont tableaunumerique.net, concours-atsem.fr, trouvix.fr ou encore laboiteaconcours.com Frédéric fait partie du collectif Profbook.fr.
Besoin de cours particuliers ou d’une remise à niveau en maths ? C’est ici ! Cours particuliers de Mathématiques et de français à distance et en présentiel niveau primaire, collège et Prépa Concours
















